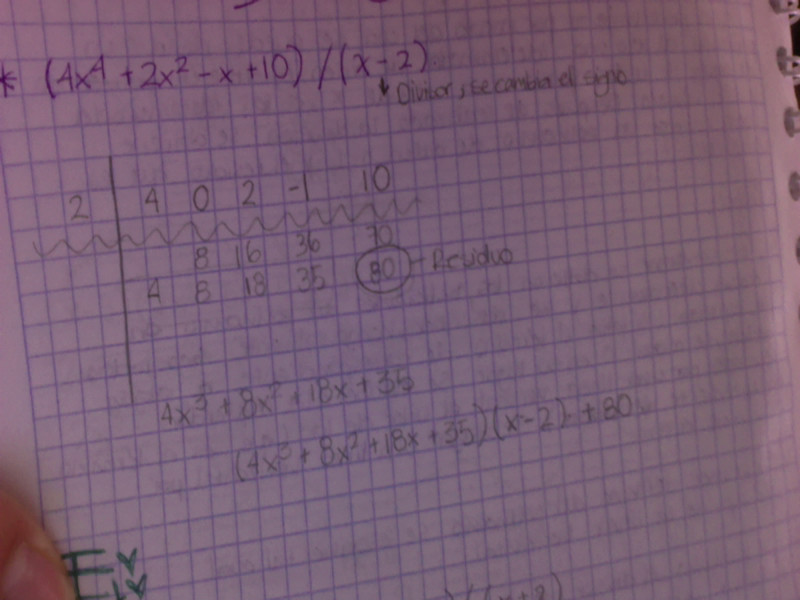Gráficas de las funciones trigonométricas

la forma completa de una función seno es: f(x) igual a Asen por (Bx más C) más D

donde:
a: es mi amplitud
b: es mi periodo
c: desplazamiento horizontal
d: desplazamiento vertical

El periodo es el tiempo que tarda la gráfica en cumplir con un ciclo y se obtiene T es igual a 2pi sobre B.

Ángulo de elevación y depresión

El ángulo formado por la horizontal y el objeto que se sitúa por arriba de ésta se le conoce como ángulo de elevación.

Si el objeto se encuentra por debajo de la horizontal se le llamará ángulo de depresión…

Ejemplo: determina la altura de un poste vertical, si su sombra mide 16.09m, cuando la altura del sol sobre la horizontal forma un ángulo de 47.4·

Longitud de arco

En un círculo con radio r, un ángulo central de ⊲ radianes intersecta un ángulo de longitud S1, la longitud del arco se obtienen multiplicando el radio por el ángulo central.

S es igual a r por el ángulo central.

Relación entre grados y gradianes

Un radián se define como la medida del ángulo central de un arco de igual longitud que el radio del círculo.

Para poder convertir radianes a grados se multiplican los radianes por (180/⫪)
 Por ejemplo: convertir 3 radianes a grados:

3/1 (180/pi) es igual a 171.88 grados

Para convertir de grados a radianes, se tienen que multiplicar los grados por (pi/180).
Por ejemplo, convertir a radianes los siguientes grados: 240 es igual a 4.18.

Unidad 3 - Funciones Trigonométricas

El objetivo de las funciones trigonométricas es resolver problemas de magnitudes angulares y los elementos desconocidos de un triángulo.

Cuando un triángulo es rectángulo podemos obtener las 6 funciones trigonométricas y aplicar el teorema de pitágoras para encontrar sus elementos.

Existen 6 funciones trigonométricas y se obtienen de la siguiente forma:

En un triángulo rectángulo se define como seno de un ángulo agudo al valor obtenido al dividir la longitud del cateto opuesto al ángulo entre la longitud de la hipotenusa.
Se define como coseno de un ángulo agudo al valor obtenido al dividir la longitud del cateto contiguo al ángulo entre la longitud de la hipotenusa.
Se define como tangente de un ángulo agudo de un triángulo rectángulo al valor del cociente obtenido al dividir la longitud del cateto opuesto entre la longitud del cateto contiguo.

sen(B) = AC/BC
cos(B) = BA/BC
tan(B) = AC/BA

Funciones con radicales

Una función con radical se asocia generalmente con problemas de asistencia y relación entre potencias entre 2 variables, por ejemplo, al determinar una distancia, aplicando el teorema de pitágoras.

Elaborar la gráfica con radicales:

k (x) = √ 25 - x⋀2

Asintotas

Asintota vertical: es la recta a la que se le aproxima una curva a medida que a x toma valores cada vez más cercanos las raíces del numerador sin llegar a tocarla.

Asíntota horizontal: es una recta a la que a la curva se aproxima a medida que x toma valores de - infinito y + infinito.


Cuando tienes dos asíntotas verticales es importante al momento de anotar el rango unir cada una con una U que quiere decir que está unida a las demás ramas.

En el caso de esta tabulación y gráfica, en donde mis asintotas verticales son las azules y la horizontal pegada casi al eje x es morada… podemos notar que son 3 ramas, entonces estas se tendrán que unir entre si.

Mi dominio será: todos los números reales excepto 4, 2 y -3
El rango será: todos los números reales excepto 0.1 y se unirán de esta manera:

( - infinito, -3⦘U ⦗-3,2⦘ U ⦗4, + infinito)

se puede notar que lo que ponemos en el rango son los dominios unidos de rama a rama.

Dominio, Rango, Número de ramas y continuidad de...

Como ya sabemos, el dominio lo sacamos desde mi ecuación en este caso, mi ecuación será:

2x - 1 / x⋀2 - 9

Mi dominio serán todos los Reales excepto 3 y -3. Así que tendré dos asintotas verticales.

Mi gráfica tendrá una rama y el rango lo mediré de acuerdo al punto más alto de mi gráfica y al otro punto más cerca de mi asintota horizontal, en este caso, mi rango será de: (.5, 8.5) que va desde ( - infinito, 3⦘ y ⦗3, +infinito).

Continuidad en las funciones

Mi continuidad de una función va a partír de mi asintota vertical, desde mi asintota vertical que es 2 hacia el lado izquierdo va a quedar:

 (-infinito, 2⦘

y hacia el lado derecho quedará:

⦗2, + infinito)

El corchete significa que es donde va a parar el infinito, mientras que el paréntesis significa que continua.

Gráficas de una función racional

Para analizar la gráfica de una función, debemos obtener las raíces del numerador para conocer los puntos importantes de esta.

Ejemplo: 3/x-2

Para traficar, es importante saber que el dominio de las raíces o sea 2, no se va a poder traficar, sólo es un punto para partir a traficar, se deben de contar 3 números hacia arriba pero claro que queden todos cerca del 2 los primeros números al estar cerca, tienen que ser decimales .
Al terminar la gráfica es importante trazar mi asintota vertical, que nuevamente es 2.

UNIDAD 2. Funciones con Radicales y Racionales

Funciones con números racionales

Al igual que las funciones polinomeales se pueden graficar, sólo que en este tipo de funciones el eje no corta al de eje de las x, por lo tanto NO hay raíces.

Ejemplo: Graficar la función f(x) = 1/x

f(-4) = - 1/4 = -.25

X    Y                                   
-4   -.25
-3   -.33
-2    -.5
-1    -1
0    ERROR
1    1
2    .5
3    .33
4    .25

Una función racional h(x) es el cociente de 2 funciones f(x) y g(x) :  h(x)= f(x)/g(x)

Donde f(x) y g(x) son funciones polinomeales y se debe cumplir que g(x) sea diferente de 0, lo cual se significa que los valores donde g(x) sea igual a cero no pertenecerán a la función y el dominio serán todos los reales, excepto esos valores.

Ejemplo: 

Determinar dominio de la función f(x)= 3/x-2

g(x)= x - 2 = 0

               x=0

 D: R - (2)

Análisis del comportamiento gráfico de una función polinomeal

 Si el grado mayor de un polinomio es impar, pueden existir 2 posibilidades:

a) si a es positivo las gráficas serán crecientes.

b) si el valor de a es negativo, la gráfica va a decaer.

Si el grado mayor es par, se tiene 2 posibilidades:

a) si a es positivo las ramas de la gráfica abrirán hacia arriba.

b) si el valor de a es negativo, las ramas abren hacia abajo.

 

- Una función polinomeal tiene la característica de ser siempre continua sin interrupciones a lo largo de su trayectoria en todo su dominio, es decir, el dominio son todos los reales.

Raíces y gráfica de una función de 4to grado

Para obtener las raíces de esta función se aplica el mismo método que para las funciones de tercer grado, sólo que esta vez se tendrá que dividir dos veces.

Ejemplo: obtener raíces y gráfica de la función:

x⋀4 - x⋀3 - 16x⋀2 + 4x + 48 = f(x)

✶ Los factores de 48, son: ±1, ±2, ±3, ±4, ±6, ±8, ±12

✶ Sustituimos uno de los factores en la ecuación, en este caso será dos.

✶ Se divide la ecuación entre ese factor, es necesario cambiarle el signo al contrario.

✶ Ahora hay que buscar otro factor, en este caso 4 y volvemos a dividir.

✶ Graficamos con números cerca a los factores 

Ecuaciones cúbicas

Si multiplicamos 2 o más binomios obtenemos una ecuación de primero o segundo grado, al multiplicar un binomio obtendremos una ecuación de n grados.

(x+a) (x+b)

x(x)+x(b)+a(x)+a(b)

x⋀2 + x (b+a) + ab

Efectuar la multiplicación del binomio de (x+2) (x-3) = x⋀2-x-6

Si se conoce la expresión cúbica para conocer los factores de una fracción debes obtener las raíces de la expresión:

Por ejemplo:  f(x) = x⋀3 + 3x⋀2 - 4x -12    → función

                         0 = x∧3 + 3x⋀2 - 4x -12     → ecuación

✿ Se obtienen los factores del término sin x, en este caso -12, ¿qué números se pueden multiplicar para que salga -12?

±1, ±2, ±3, ±4, ±6, ±12

(-3)(1)(4)= -12

(6)(1)(-2)= -12

….. y muchos más

✿ Se sustituyen uno de los factores (el que sea). En este caso 1. Es importante que el número que sustituyamos de 0 en la ecuación.

✿ Dividimos la ecuación entre el factor x-2 y comprobamos.

✿ Por último efectuamos la gráfica: 

División sintética

La división sintética es un algoritmo para rápidamente dividir polinomios cuando el divisor está en el x-r de la forma. La división sintética formalmente se llama la regla de Ruffini. La división sintética es de uso general verificar raíces de un polinomio.

Pasos para llevar a cabo la división sintética:

1. Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta

2. Después escribimos “c” en la parte derecha del renglón

3. Se baja el coeficiente de la izquierda al tercer renglón.

4. Multiplicamos este coeficiente por “c” para obtener el primer numero del segundo renglón (en el primer espacio de la izquierda nunca se escribe nada).

5. Simplificamos de manera vertical para obtener el segundo número de el tercer renglón.

6. Con este último número repetimos los pasos cuatro y cinco hasta encontrar el último número del tercer renglón, que será el residuo.

Por ejemplo: 

División de polinomios

La comprobación de una división se efectúa de la siguiente manera:

(cociente)(divisor) + residuo = dividendo

Algunas ecuaciones de grado superior A2 se pueden factorial en dos o más términos que nos permiten reducir las expresiones de forma más sencilla para resolverlas.

ejemplo: dividir el polinomio 3x⋀2 + x - 1 entre el binomio x+2

La división se efectúa de la misma manera que una división normal.

Ecuaciones Bicuadráticas

Una ecuación bicuadrática es una ecuación de cuarto grado que sólo tiene términos x⋀4, x⋀2 y el término constante.

Para traficarla podemos transformarla en una ec. cuadrática y encontrar sus soluciones.

Ejemplo: Graficar la ec. bicuadrática: x⋀4-2x⋀2-8 = 0

x⋀4→ y⋀2

x⋀2→ y

Vamos a sustituir la ecuación pero ahora con y, de acuerdo con las igualdades que están arriba, quedaría:

y⋀2-2y-8=0

Tenemos que buscar dos números que sumados den -2 y multiplicados -8. Los dos números serán -4 y 2

Factorizamos:

(y+2) (y-4) = 0

y+2=0

y= -2

y-4=0

y=4

y=x⋀2 y sustituimos

 x⋀2= -2                         x⋀2= 4

Sacamos sus respectivas raíces, la primera será imaginaria; entonces tenemos:

x1= 2      x2= -2

Y graficamos:

Análisis del discriminante

Análisis del discriminante:

raíz cuadrada de b - 4ac

Cuando el discriminante es mayor a 0 se obtienen 2 soluciones diferentes y el eje de las abscisas x, se corta dos veces; b - 4ac > 0

Cuando el discriminante es igual a 0, obtendremos 2 soluciones iguales y el eje x se corta una vez y es tangente al vértice; b - 4ac = 0

Cuando el discriminante es menor a 0 la solución son dos raíces complejas y conjugadas y no corta al eje x en ningún punto; b - 4ac < 0

Ejemplo:

Obtención de los ceros o raíces de las funciones polinomeales

a) Ecuación cuadrática  ax2+bx+c=0

ejemplo: obtener las raíces de la ec x∧2+x+6=0

- 2 números que sumados sean igual a b
- multiplicados =c =-b

Los números son 3 y -2 (vamos a factorizar)

(x+3)      (x-2) = 0
x+3=0     x-2=0
x1= 3       x2= 2


xv= -b/2a
xv= -(1)/2 = -.5

yv= (-.5)(-.5) + (-.5) - 6 = 6.25

Función Polinomeal

Una función polinomeal tiene la forma:

f(x) = a_nXⁿ + a_{n1 − 1}Xⁿ − 1 + a_{n − 2}Xⁿ − 2 + ... + a₁ + a₀ 

En donde ¨n¨ es un número entero positivo.

El dominio de una función polinomeal, siempre va a ser el conjunto de los reales: R


a) Función de la forma:  f(x) = a0

Está función es una constante y su gráfica es una línea recta horizontal, situada en a0.
- La gráfica será horizontal paralela a el eje x.


b) Función de la forma:  f(x)= a0+a1x1

Está nos dará como gráfica una función lineal con inclinación, dependiendo de a1 será negativa (izquierda) o positiva (derecha).


c) Forma: f(x)= a0+a1x1+a2x2

Está función nos da una gráfica en forma de parábola, ya que representa un función cuadrática y para traficarla hay que seguir estos pasos:

1. encontrar el vértice de la función a partir de la siguiente fórmula -a1/2a2. La ordenada se obtiene al sustituir el valor de x en la función.

2. sustituir algunos valores que se encuentren cercarnos al valor de x (la que obtuvimos en la paso 1).

Unidad 1. Funciones Polinomerales

Una función es un conjunto de parejas ordenadas, en la cuál no puede haber relacionados dos elementos de un conjunto con un elemento del otro conjunto.

Al conjunto formado por los primeros elementos se le llama dominio y al otro conjunto se le llama contra-dominio o rango, y para establecer la asociación de los elementos del dominio con los elementos del contra-dominio, existe una regla de correspondencia.

Por ejemplo:

Alumnos    Calificación
Miguel               8
Nabil                 7
Yessica             8
Javier               10
David              NP

Mi dominio es: {Miguel, Nabil, Yessica, Javier y David}

Mi rango es: {8, 7, 8, 10, NP}

Regla de correspondencia: ¨Calificación de taller de computo¨.


Otro ejemplo:

❖ Si el kilogramo de azúcar tiene un costo de $5, ¿Cuánto se pagará por 2, 3, 4.5, 5 y 6.5 kg respectivamente?

Tenemos que, mi dominio será: {2, 3, 4.5, 5 y 6.5}

Y obtendremos el rango de la siguiente manera: f(x) = 5x
2x5= 10
3x5= 15
4.5x5= 22.5
5x5= 25
6.5x5= 32.5

Rango: {10, 15, 22.5, 25, 32.5}

Regla de correspondencia: ¨Precio por kg¨


► Entonces tenemos que una función es una regla de correspondencia en la que a todo elemento del conjunto D (dominio) está asociada con 1 y sólo 1 de los elementos del rango.

Para detonar una función se emplea la sig. expresión:  f: A→B
Y la regla de correspondencia se establece por medio de la expresión:  f(x)